1. Задание № 266 

Сложность: III
Классификатор алгебры: 5\.10\. Прочие логарифмические неравенства
Методы алгебры: Замена переменной
Логарифмические неравенства
i
Найдите сумму наименьшего и наибольшего целых решений неравенства 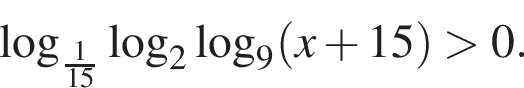
Решение. ОДЗ: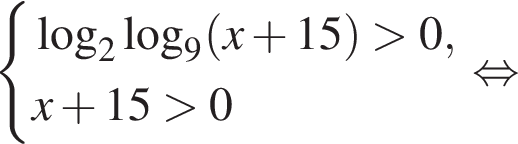
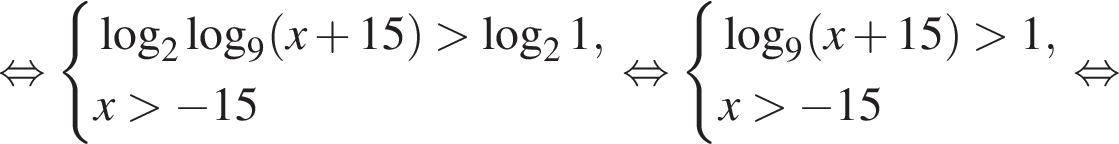
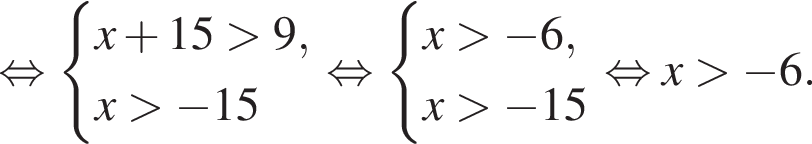
Последовательно решим неравенство. Пусть 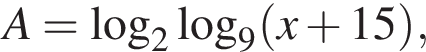 тогда:
тогда:
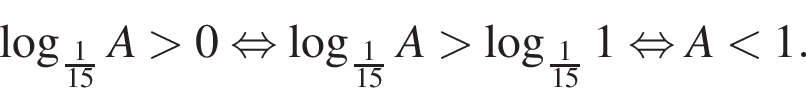
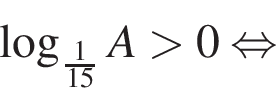
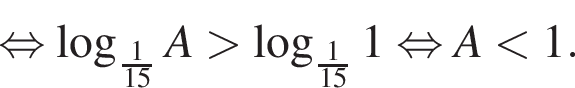
Вернемся к A:

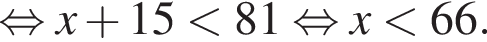


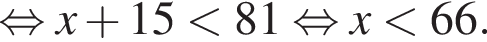
C учетом ОДЗ имеем 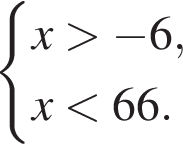 Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Ответ: 60.
Ответ: 60
266
60
Сложность: III
Классификатор алгебры: 5\.10\. Прочие логарифмические неравенства
Методы алгебры: Замена переменной
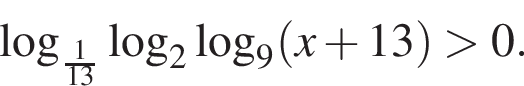
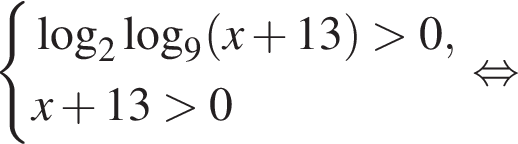
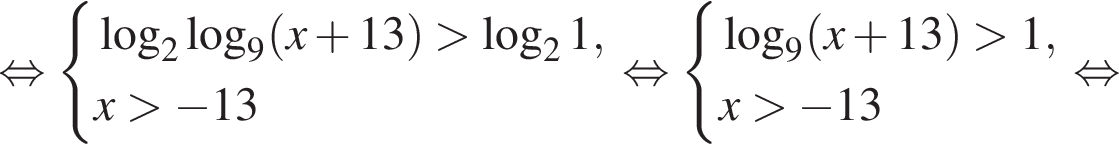
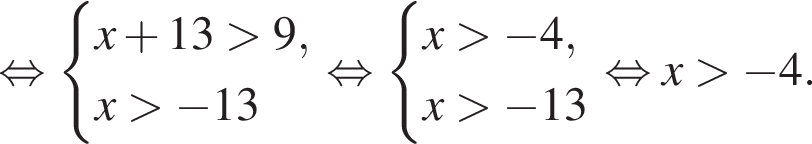
 тогда:
тогда: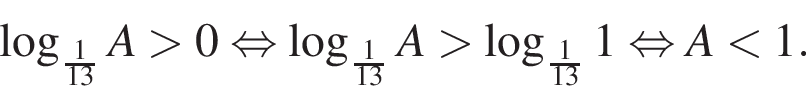
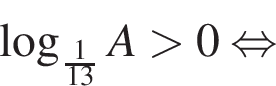
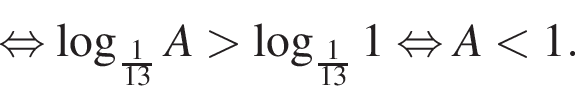

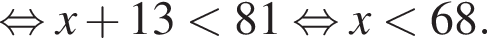

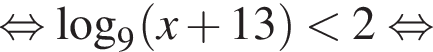
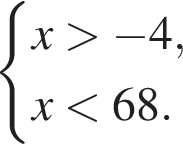 Поэтому наибольшее целое значение — 67, наименьшее целое значение −3, их сумма равна 64.
Поэтому наибольшее целое значение — 67, наименьшее целое значение −3, их сумма равна 64.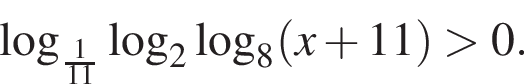
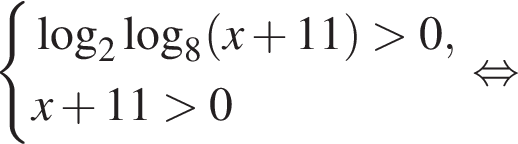
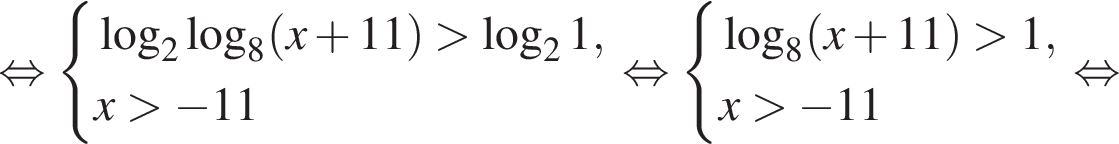
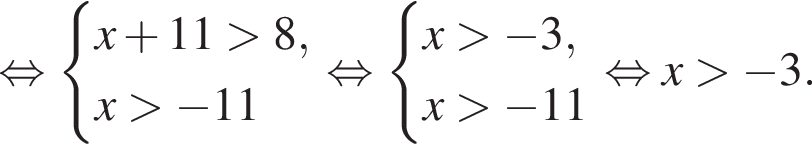
 тогда:
тогда: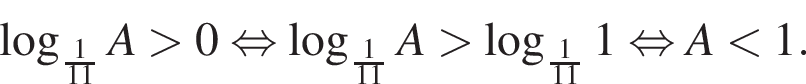
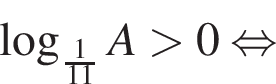
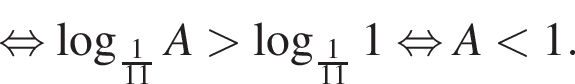



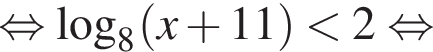
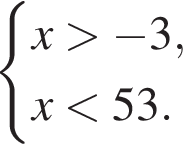 Поэтому наибольшее целое значение — 52, наименьшее целое значение −2, их сумма равна 50.
Поэтому наибольшее целое значение — 52, наименьшее целое значение −2, их сумма равна 50.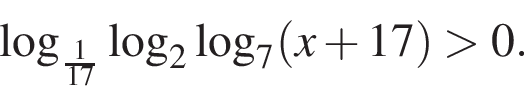

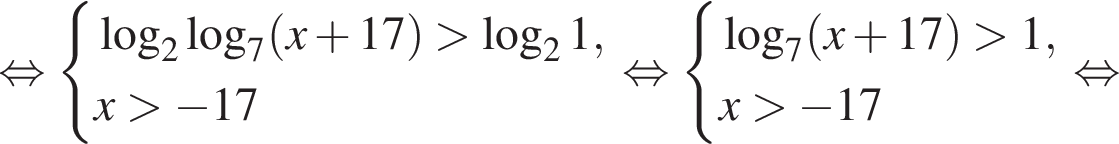
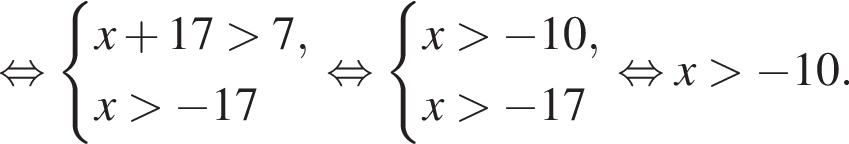
 тогда:
тогда: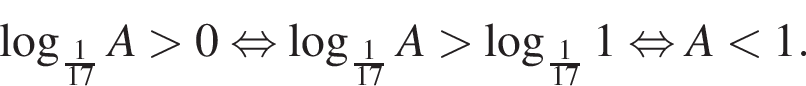
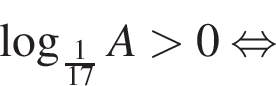
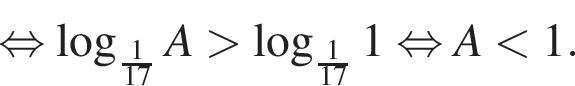

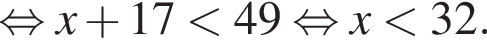

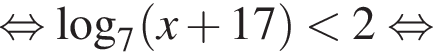
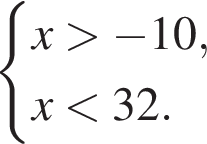 Поэтому наибольшее целое значение — 31, наименьшее целое значение −9, их сумма равна 22.
Поэтому наибольшее целое значение — 31, наименьшее целое значение −9, их сумма равна 22.
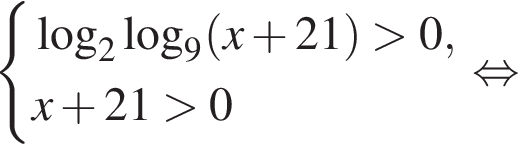
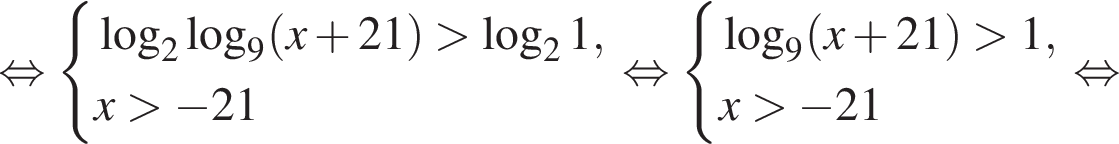
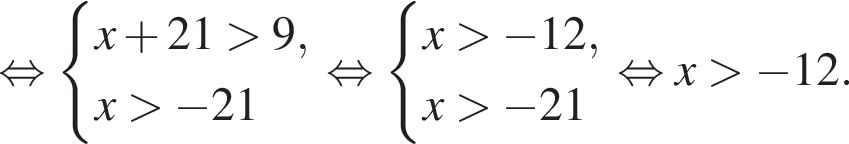
 тогда:
тогда: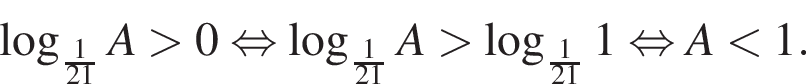
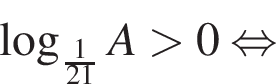
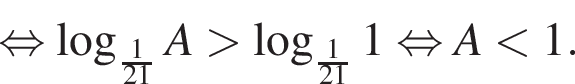

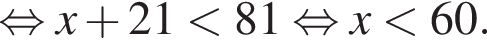

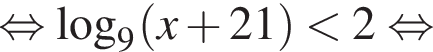
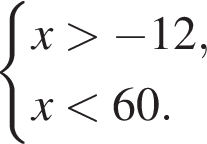 Поэтому наибольшее целое значение — 59, наименьшее целое значение −11, их сумма равна 48.
Поэтому наибольшее целое значение — 59, наименьшее целое значение −11, их сумма равна 48.